Calculo Diferencial
José Eugenio Mata Villalobos
No.Control:15261098
UNIDAD 4: Derivadas.
No.Control:15261098
UNIDAD 4: Derivadas.
4.1 Conceptos de incremento y razón de cambio. La derivada de una función.
INCREMENTO.-Cuando una cantidad variable pasa de un valor inicial a otro valor, se dice que ha tenido un incremento. Para calcular este incremento basta con hallar la diferencia entre el valor final y el inicial. Para denotar esta diferencia se utiliza el símbolo ∆x, que se lee "delta x". El incremento puede ser positivo o negativo, dependiendo de si la variable aumenta o disminuye al pasar de un valor a otro.
RAZÓN DE CAMBIO.-Comenzando por la Razón Instantánea de Cambio de una función cuya variable independiente es el tiempo t. suponiendo que Q es una cantidad que varía con respecto del tiempo t, escribiendo Q=f(t), siendo el valor de Q en el instante t.
DERIVADA DE UNA FUNCIÓN.-La derivada de cualquier función, no solamente una función del tiempo, puede interpretarse como una razón de cambio instantánea con respecto de la variable independiente. Si y=f(x), entonces la razón de cambio promedio de y (por un cambio unitario en x) en el intervalo [x,x+∆x] es el cociente
4.2 La interpretación geométrica de la derivada.
La Interpretación Geométrica de la Derivada

4.3 Conceptos de diferencial, interpretacion geometrica de los diferenciales
La forma en que hemos abordado el concepto de derivada, aunque existen varios conceptos, fue el encontrar la relación de la pendiente de la línea recta y´ =f ´(x) que era tangente a la función. Para un punto en particular podemos llegar a la definición de la derivada f ‘(x) y vimos que f ‘(x1) es la pendiente de la recta tangente a la curva en x=x1.
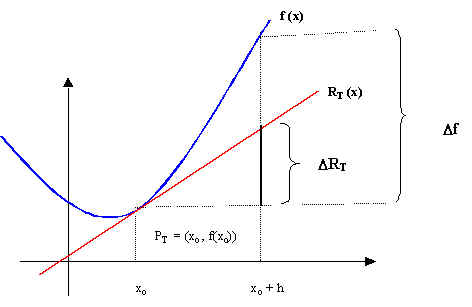
El diferencial se puede tomar en el sentido geométrico como la elevación de la tangente desde el punto en que se toma el diferencial.
Recuérdese que la derivada de la función en el punto es la pendiente de la recta tangente a la función en el punto, como sabemos que la tangente de un ángulo es igual al cociente entre el cateto opuesto (incremento de y) y el cateto contiguo (incremento de x) de un hipotético triángulo rectángulo, sólo hay que despejar el incremento de y que equivale a nuestro diferencial.
Vista geométricamente, la elevación se produce verticalmente a partir del punto en que se toma el diferencial. El incremento que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.
que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.
Así la elevación de la tangente que se obtenga como resultado dependerá del punto en cuestión y del alejamiento horizontal que se tomen, que en la formulas matemáticas están definidos respectivamente por y
y  .
.
4.4 Propiedades de la derivada.


4.5 Regla de la cadena.












4.6 Formulas de derivación y formulas de diferenciación










Solución:
 ;
;

INCREMENTO.-Cuando una cantidad variable pasa de un valor inicial a otro valor, se dice que ha tenido un incremento. Para calcular este incremento basta con hallar la diferencia entre el valor final y el inicial. Para denotar esta diferencia se utiliza el símbolo ∆x, que se lee "delta x". El incremento puede ser positivo o negativo, dependiendo de si la variable aumenta o disminuye al pasar de un valor a otro.
RAZÓN DE CAMBIO.-Comenzando por la Razón Instantánea de Cambio de una función cuya variable independiente es el tiempo t. suponiendo que Q es una cantidad que varía con respecto del tiempo t, escribiendo Q=f(t), siendo el valor de Q en el instante t.
DERIVADA DE UNA FUNCIÓN.-La derivada de cualquier función, no solamente una función del tiempo, puede interpretarse como una razón de cambio instantánea con respecto de la variable independiente. Si y=f(x), entonces la razón de cambio promedio de y (por un cambio unitario en x) en el intervalo [x,x+∆x] es el cociente
4.2 La interpretación geométrica de la derivada.
La Interpretación Geométrica de la Derivada
Además de evaluar el valor de una función en cierto punto, también es esencial que evaluemos la variación en el valor de la función a medida que la entrada de la función varía. Esto se conoce como la pendiente de la recta en el caso de una recta lineal. Mientras que para una recta curva, la pendiente de la recta varía en cada punto.
Esto significa que para una línea recta / función lineal se obtiene un número constante como su pendiente. Mientras que para una recta curva la pendiente es una función del valor de entrada de la función.
La noción de derivada puede explicarse de dos maneras, una como la pendiente de la curva, que es la representación geométrica, y la otra como la tasa de variación, que es la representación física. La pendiente de la tangente de la curva extrae la derivada de la función geométrica.
Supongamos que una función f(x) = x2. La gráfica de la función luciría de la siguiente forma

4.3 Conceptos de diferencial, interpretacion geometrica de los diferenciales
La forma en que hemos abordado el concepto de derivada, aunque existen varios conceptos, fue el encontrar la relación de la pendiente de la línea recta y´ =f ´(x) que era tangente a la función. Para un punto en particular podemos llegar a la definición de la derivada f ‘(x) y vimos que f ‘(x1) es la pendiente de la recta tangente a la curva en x=x1.
El diferencial se puede tomar en el sentido geométrico como la elevación de la tangente desde el punto en que se toma el diferencial.
Recuérdese que la derivada de la función en el punto es la pendiente de la recta tangente a la función en el punto, como sabemos que la tangente de un ángulo es igual al cociente entre el cateto opuesto (incremento de y) y el cateto contiguo (incremento de x) de un hipotético triángulo rectángulo, sólo hay que despejar el incremento de y que equivale a nuestro diferencial.
Vista geométricamente, la elevación se produce verticalmente a partir del punto en que se toma el diferencial. El incremento
 que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.
que se tome representará el alejamiento horizontal que haga desde el punto en cuestión. Así la elevación de la tangente que se obtenga como resultado dependerá del punto en cuestión y del alejamiento horizontal que se tomen, que en la formulas matemáticas están definidos respectivamente por
 y
y  .
. 
4.4 Propiedades de la derivada.


4.5 Regla de la cadena.
Esta propiedad asegura que si y = f(x) es una función derivable en un cierto intervalo I,
y z = g(y) es otra función derivable y definida en otro intervalo que contiene a todos los valores (imágenes) de la función f,
entonces la función compuesta
definida por (g o f) (x) = g[f(x)], es derivable en todo punto x de I y se obtiene
Ejemplo: cálculo de derivadas
-------------------------------------------------------------------------------------------------------------------------
Calcular la derivada de la función h(x) = sen x2.
Resolución:
· La función sen x2 es una función compuesta de otras dos f(x) = x2 y g(x) = sen x.
· Al ser g(x) = sen x, g'(x) = cos x, por tanto g'[f(x)] = cos f(x) = cos x2
· Por la regla de la cadena,
h'(x) = g'[f(x)] · f'(x) = 2x cos x2
Resolución:
· De g(x) = x3, se deduce g'(x) = 3x2. En consecuencia,
· Por la regla de la cadena,
4.6 Formulas de derivación y formulas de diferenciación



2. 


3. 


4. 


5. 


4.7 Derivadas de orden Superior, regla de L'Hopitall
Derivadas de Orden Superior y Regla de L’Hôspital
La derivada de cualquier función determina la tasa de variación en función de la función con respecto a la entrada de la función. Este proceso de encontrar la derivada de una función se puede aplicar en una cascada muchas veces para encontrar las derivadas de orden superior de la función. Por ejemplo, al diferenciar la derivada de primer orden de la función, uno obtendrá la derivada de segundo orden de la función y a través de la diferenciación de la derivada de segundo orden de la función obtendremos la derivada de tercer orden de la función y así sucesivamente. En términos simples diferenciar la derivada de una función dará lugar a una derivada de la función de orden superior por un grado. La derivada de primer orden de la función se representa como,
La regla de L’Hôspital, también llamada regla de Bernoulli es una parte muy importante del cálculo. Se utiliza principalmente para encontrar las salidas de los límites cuando los límites son de forma intermedia; se utiliza principalmente para las derivadas de las funciones.

Ejemplos:
1- 

2-

3-


4-
4.8 Derivadas de funciones implícitas.
Derivada de las Funciones Implícitas
Las funciones se pueden clasificar en dos categorías generales, funciones implícitas y funciones explícitas.
Una función se denomina implícita cuando su salida no está definida en términos de su entrada, explícitamente.
Las funciones algebraicas y las funciones inversas corresponden a la categoría de funciones implícitas.
Una función que se define implícitamente puede ser diferenciada con la ayuda de una regla de la cadena, denominada diferenciación implícita.
La mejor forma de diferenciar una función implícita es diferenciando cada lado de la ecuación de la función explícitamente.
Mientras se hace esto, es esencial tener en mente que la variable dependiente de la función debe ser tratada como la variable independiente de la función; y sencillamente aplicar las reglas de diferenciación normal incluyendo todas las propiedades y las reglas de diferenciación.
Ejemplos:

4- Calcula y', siendo
Solución:
Tenemos: 
hallamos las derivadas parciales:
Por lo tanto:
Bibliografía:
-http://www.vitutor.com
-http://mitecnologico.com
-http://mitecnologico.com
-http://www.virtual.unal.edu.co
-Imagenes Google.
-Imagenes Google.